​参考：西湖大学赵世钰老师的【强化学习的数学原理】

强化学习

机器学习（Machine Learning, ML）分为监督学习，非监督学习，以及半监督学习，其中非监督学习里又包含有自监督学习，除去这些以外，强化学习（Reinforcement Learning, RL）也作为机器学习的一种，但是其重点在于学习策略而非结果。

举个种菜的例子，一般的机器学习都是正向地预测目标，比如这里水，CO2，营养液，风扇速率等各种变量构成了机器学习中的参数，我们需要训练模型，使其通过这些参数去预测出一个最终可能的产量或者重量等结果。但是，对于强化学习来说，它的目标在于如何去找到一个最佳的策略（什么时候加水？加多少水？风扇什么时候开？），使其产量达到最高，因此我们可以说强化学习不是预测结果，而是要去指导每一个阶段的动作。

目前RL应用于很多领域，包括但不限于：

• 游戏
• 自动驾驶
• 股票金融
• 能源管控

术语/概念介绍

核心概念

强化学习中有几个核心概念，分别是智能体（agent），状态（state），行为（action），策略（policy），奖励（reward）。比较书面的解释为：

• 智能体：是指能够感知环境并采取行动以实现特定目标的代理体。它通过感知环境中的变化（如通过传感器或数据输入），根据自身学习到的知识和算法进行判断和决策，进而执行动作以影响环境或达到预定的目标。
• 状态：描述了智能体在当前环境的一个状态，环境基本上代表了这个情境里里所有的参数。
• 行为：智能体可以采取的行为。
• 策略：告诉智能体在哪个阶段采取什么样的行为。
• 奖励：在智能体采取某一个行为之后，会获得奖励，也可以叫做环境给予的反馈。

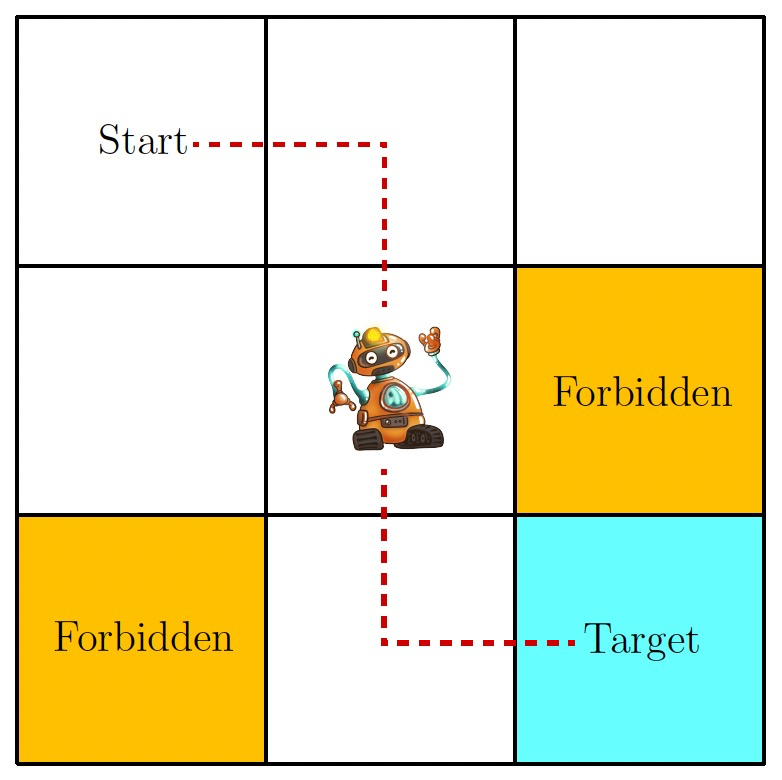
拿最经典的网格游戏为例，如图，机器人会在其中一个网格，最终目标是找到一条最优路径去到Target space，其中有障碍物Forbidden。那么这里的最优路径也就是我们要寻找的策略，机器人便是智能体，它每一个时刻所处的格子为他的状态，然后在不同的状态下它可以选择不同的上下左右四种行为，这样就描述了一个完整的任务。

但是强化学习的过程学习的是什么东西呢？我们都知道在机器学习中，存在一个loss函数，描述了预测值到真实值之间的距离，我们的目标就是使其减少或者是尽可能收敛。但在强化学习中，采用了另一种方式来指导模型自我迭代，那就是奖励，智能体每做一次行为之后都会得到奖励，如果这个奖励是负数的话也可以被叫做惩罚，强化学习的目标就是最大化所获得的奖励。

除此以外，还有返回（Return）和马尔可夫决策过程（Markov decision processes, MDP），返回指的是一条路径上所获得的奖励之和，马尔可夫决策过程单开一章详细解释。

马尔可夫决策过程

以下统一用MDP表示

MDP是一种正式的方式去表示上述描述的所有内容，是离散时间随机控制过程，它提供了一个数学框架：

• 集合（Sets）
  • 状态空间（State space），写作\(\mathcal{S}\)。
  • 行为空间（Action space），写作\(\mathcal{A}(s)\)，\(s \in \mathcal{S}\)，因为行为与当前状态相关。
  • 奖励集（Reward set），写作\(\mathcal{R}(s,a)\), 奖励与当前状态和所选行为相关。
• 模型（Model）
  • 状态转移概率（State transmission probality）：从一个状态s经过某个行为a转移到另一个状态s’的概率\( p(s^’|s,a)\) ，其中\( \sum_{s^’ \in \mathcal{S}}p(s^’|s,a) = 1\)。
  • 奖励概率（Reward probability）：在状态s时，当我们选择行为a，所能获得奖励r的概率为\(p(r|s,a)\)，对于每一个状态和动作都有\(\sum_{r \in \mathcal{R}(s,a)}p(r|s,a)=1\)
• 策略（Policy）：在状态s中选择某个行为a的概率为\(\pi (a|s)\), 对于每一个状态都有\(\sum_{a \in \mathcal{A}(s)} \pi (a|s)=1\)
• 马尔可夫特性（Markov property）：其实就是无记忆性，任何时刻可能采取的行为与之前的所有行为都无关，只与当下有关，记住就行。具体的数学表达式为： $$ p(s_{t+1}|s_t,a_t,s_{t-1},a_{t-1},…,s_0,a_0) = p(s_{t+1}|s_t,a_t) $$ $$ p(r_{t+1}|s_t,a_t,s_{t-1},a_{t-1},…,s_0,a_0) = p(r_{t+1}|s_t,a_t) $$