$$ \begin{align*} v_\pi(s) &= \sum_{a \in \mathcal{A}} \pi(a|s) \sum_{r \in \mathcal{R}}p(r|s,a)r + \lambda \sum_{s’ \in \mathcal{S}}v_\pi(s’)\sum_{a \in \mathcal{A}} p[s’|s,a]\pi(a|s) \\ &= \sum_{a \in \mathcal{A}}\pi(a|s)[\sum_{r \in \mathcal{R}}p(r|s,a)r+\lambda \sum_{s’ \in \mathcal{S}}v_\pi(s’)p[s’|s,a]] \end{align*} $$

​参考：西湖大学赵世钰老师的【强化学习的数学原理】

Return 和 State value

如上一章所讲，强化学习就是学习一个好的Policy的过程，那如何量化这个Policy是不是好的呢，于是引出了Reward的概念。但是Reward只能体现智能体在某一个状态下可以做的行为的好坏，而并不能体现出全局的思想，而策略可以看作一系列行为的集合，包括在每一个状态下怎么去行为。上一章还写到了Return的概念，也就是一条路径上所有奖励的和。

如何计算Return？还是拿网格游戏举例子，如图定义了一个2x2的地图，初始状态是\(s_1\)，我们需要找到一条道路去到\(s_4\)，我们定义黄色的方格为禁区，如果到达禁区，奖励为-1，到达空白区域奖励为0，到达目的地奖励为1。

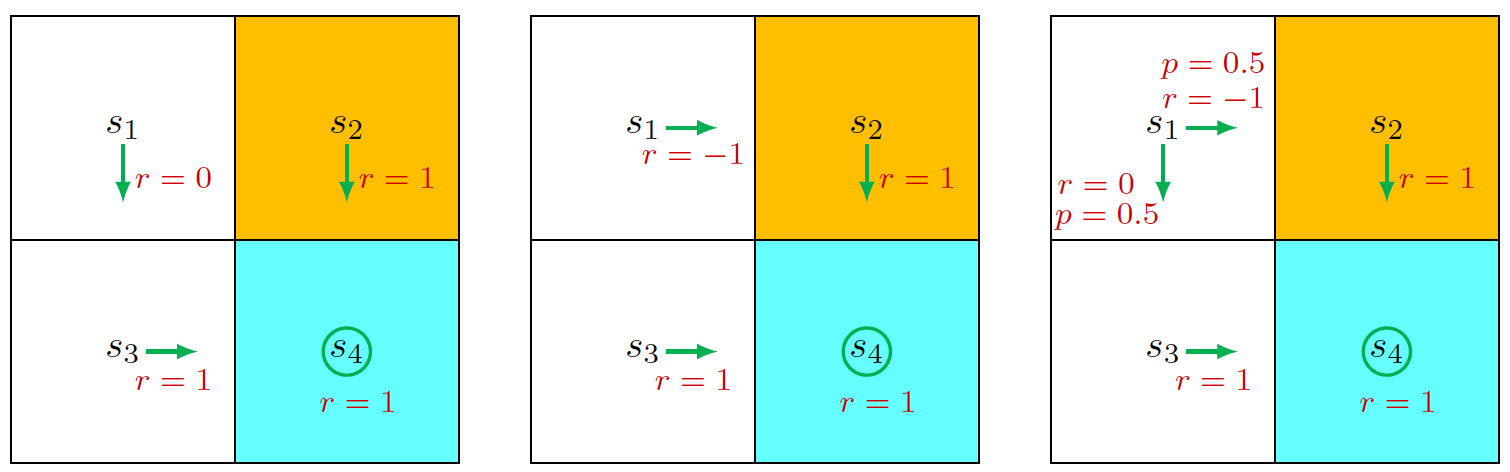
我们设定智能体会一直运作下去，到了target space也不停下来。如图定义了三种不同的策略，箭头代表了每一个状态下的行为，那么状态\(s_1\)在前两个策略下的Return为（用\(G\)来表示，利用无穷等比数列的求和公式）：

$$ G_1 = \begin{cases} \begin{align*} 0 + 1 \cdot \lambda + 1 \cdot \lambda^2 + 1 \cdot \lambda^3 + \ldots &= \frac{\lambda}{1 - \lambda} \\ -1 + 1 \cdot \lambda + 1 \cdot \lambda^2 + 1 \cdot \lambda^3 + \ldots &= -1 + \frac{\lambda}{1 - \lambda} \end{align*} \end{cases}, \quad \lambda \in (0,1) $$

Return并不单纯只是路径上所有Reward之和相加，而是加入\(\lambda\)作为权重，目的是为了限制Return不会无休止地膨胀下去，并且我们可以通过控制其大小来控制模型的“远视”或者“近视”，如果\(\lambda\)偏向1，那么模型将会看得更远，如果偏向0，那么权重衰减得将会很快，模型会更看重前面几个状态的抉择。

但是这是在策略固定的情况下，也就是说我们知道在每一个状态，有且只有一个行为可以选择。

然而，在真正的学习过程中，策略是不固定的，也就是说每一个状态下都有多个行为可以选择，我们需要求得最优解，即每个状态下走哪一条路的概率最高，于是我们引出了状态值（State value）的概念。很简单，其实状态值就是该状态下可能的所有路径的Return的期望。所以在前两种策略下，\(s_1\)的State value就等于它的Return，而第三种策略下，其状态值为：

$$ v_1 = 0.5 * \frac{\lambda}{1-\lambda} + 0.5 * (-1 + \frac{\lambda}{1-\lambda}) = -0.5 + \frac{\lambda}{1-\lambda} $$

通过对比三种策略下\(s_1\)的状态值，我们可以得出第一种是最高的，因此第一种策略是最优策略，直观上我们也可以看出来，因为它避免了智能体进入禁区。因此这也是为什么状态值可以成为量化策略的一个指标。

贝尔曼方程

简单理解

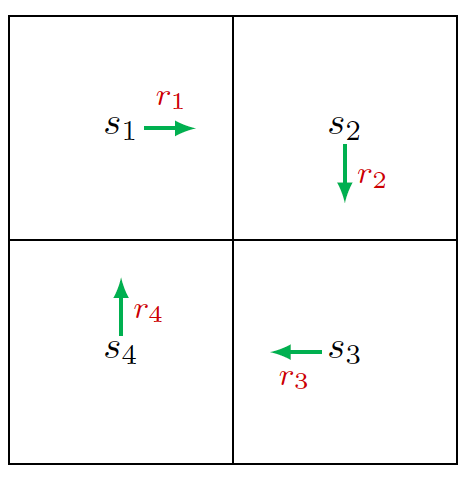
考虑一个特殊的策略，如图形成了一个循环的策略，那么我们可以求得每一个状态下的状态值为：

$$ v_1 = r_1 + \lambda r_2 + \lambda^2 r_3 + … \\ v_2 = r_2 + \lambda r_3 + \lambda^2 r_4 + … \\ v_3 = r_3 + \lambda r_4 + \lambda^2 r_1 + … \\ v_4 = r_4 + \lambda r_1 + \lambda^2 r_2 + … \\ $$

进一步简化可以得到： $$ v_1 = r_1 + \lambda v_2 \\ v_2 = r_2 + \lambda v_3 \\ v_3 = r_3 + \lambda v_4 \\ v_4 = r_4 + \lambda v_1 \\ $$

四个方程四个未知数（\(r\)看作是已知的），其实是可以把\(v\)解出来的。这里体现出了自举（bootstrapping）的思想，即从自身求自身的值。当我们把这些式子化作一个线性矩阵方程便会很好理解：

$$ \begin{pmatrix} v_1 \\ v_2 \\ v_3 \\ v_4 \end{pmatrix}= \begin{pmatrix} r_1 \\ r_2 \\ r_3 \\ r_4 \end{pmatrix}+ \lambda \begin{pmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 \end{pmatrix} \begin{pmatrix} v_1 \\ v_2 \\ v_3 \\ v_4 \end{pmatrix} \tag{1} $$

化简得\(\vec{v} = \vec{r} + \lambda P \vec{v} \)， 这其实就是贝尔曼方程在这种简单策略下的的简单表达。

复杂形式

公式推导

还是先理清几个定义，我们假设在状态\(t\)的路径为：

$$ S_t \overset{A_t}{\longrightarrow} S_{t+1}, R_{t+1} \overset{A_{t+1}}{\longrightarrow} S_{t+2}, R_{t+2} … $$

• \(S_t\)：每个状态
• \(A_t\)：从\(S_t\)到\(S_{t+1}\)所需采取的行为
• \(R_{t+1}\)：采取行为\(A_t\)到达状态\(S_{t+1}\)所能得到的奖励

可以得到这条路径的Return为：

$$ G_t = R_{t+1} + \lambda R_{t+2} + \lambda^2 R_{t+3}… = R_{t+1} + \lambda G_{t+1} \tag{2} $$

那么这个状态的状态值便是在策略\(\pi\)下所有Return的期望，这就是状态值函数，有些地方把V大写： $$ \begin{align*} V_\pi(s) = v_\pi(s) &= \mathbb{E}[G_t|S_t=s] \\ &= \mathbb{E}[R_{t+1} + \lambda G_{t+1}|S_t=s] \\ &= \mathbb{E}[R_{t+1}|S_t=s] + \lambda \mathbb{E}[G_{t+1}|S_t=s] \end{align*} $$

这里有两项，我们分别对这两项进行计算，先定义三个集合：

• \(\mathcal{S}\)：所有的状态
• \(\mathcal{R}\)：所有的奖励
• \(\mathcal{A}\)：所有的动作

首先是第一项：

$$ \begin{align*} \mathbb{E}[R_{t+1}|S_t=s] &= \sum_{a \in \mathcal{A}}\pi(a|s)\mathbb{E}[R_{t+1}|S_t=s, A_t=a] \\ &= \sum_{a \in \mathcal{A}} \pi(a|s) \sum_{r \in \mathcal{R}}p(r|s,a)r \end{align*} $$

其中\(\pi(a|s)\)为在策略\(\pi\)下，在状态\(s\)，选择行为\(a\)的概率。

接着来计算第二项，其中第二步用了马尔可夫决策过程的无记忆性的特征：

$$ \begin{align*} \mathbb{E}[G_{t+1}|S_t=s] &= \sum_{s’ \in \mathcal{S}}\mathbb{E}[G_{t+1}|S_t=s, S_{t+1}=s’]p[s’|s] \\ &= \sum_{s’ \in \mathcal{S}}\mathbb{E}[G_{t+1}|S_{t+1}=s’]p[s’|s] \\ &= \sum_{s’ \in \mathcal{S}}\mathbb{E}[G_{t+1}|S_{t+1}=s’]\sum_{a \in \mathcal{A}} p[s’|s,a]\pi(a|s) \\ &= \sum_{s’ \in \mathcal{S}}v_\pi(s’)\sum_{a \in \mathcal{A}} p[s’|s,a]\pi(a|s) \end{align*} $$

最后把二者合并起来就形成了贝尔曼方程的规范版本：

$$ \begin{align*} v_\pi(s) &= \sum_{a \in \mathcal{A}} \pi(a|s) \sum_{r \in \mathcal{R}}p(r|s,a)r + \lambda \sum_{s’ \in \mathcal{S}}v_\pi(s’)\sum_{a \in \mathcal{A}} p[s’|s,a]\pi(a|s) \\ &= \sum_{a \in \mathcal{A}}\pi(a|s)[\sum_{r \in \mathcal{R}}p(r|s,a)r+\lambda \sum_{s’ \in \mathcal{S}}v_\pi(s’)p[s’|s,a]] \end{align*} \tag{3} $$

Example

看起来很复杂，其实只是因为这是一个通用的公式，如果举个简单的例子，就很清晰了。还是拿本章最开始的第一个那个例子来说，假设我们选择第一个策略，来求取它的\(v_\pi(s=1)\)，其实就是\(v_1\)。

这里策略\(\pi\)规定了只能往下走，那么只有\(\pi(a=down|s=1)=1\)，并且向下走只能到状态\(s_3\)，所以只有\(p[s_3|s_1,a=down]=1\)。因此原式等于：

$$ \begin{align*} v_1 &= \sum_{a \in \mathcal{A}}\pi(a|s)[\sum_{r \in \mathcal{R}}p(r|s,a)r+\lambda \sum_{s’ \in \mathcal{S}}v_\pi(s’)p[s’|s,a]] \\ &= \sum_{r \in \mathcal{R}}p(r|s_1,a=down)r + \lambda v_\pi(s_3) \\ &= 0 + \lambda v_\pi(s_3) \end{align*} $$

就得到了之前的简单情况下的结果。

矩阵化

以上所写的贝尔曼方程形式都是单状态形式的，因此如果我们有\(n\)个状态的话我们就可以有\(n\)个方程，就可以写成一个矩阵形式，还是先把（3）式括号合并化简为：

$$ v_\pi(s) = r_\pi(s) + \lambda \sum_{s’ \in \mathcal(S)} p_\pi(s’|s)v_\pi(s’) $$

有\(n\)个这样的式子，因此我们可以写成这种形式，其中i=1，2，3，…，n。 $$ v_\pi(s_i) = r_\pi(s_i) + \lambda \sum_{s_j \in \mathcal(S)} p_\pi(s_j|s_i)v_\pi(s_j) $$

进一步我们可以进一步化简，直接用一个矩阵代替，为什么能这么化简呢？这里可以参考（1）式理解：

$$ \begin{pmatrix} v_1 \\ v_2 \\ v_3 \\ v_4 \end{pmatrix}= \begin{pmatrix} r_1 \\ r_2 \\ r_3 \\ r_4 \end{pmatrix}+ \lambda \begin{pmatrix} p_\pi(s_1|s_1) & p_\pi(s_2|s_1) & p_\pi(s_3|s_1) & p_\pi(s_4|s_1) \\ p_\pi(s_1|s_2) & p_\pi(s_2|s_2) & p_\pi(s_3|s_2) & p_\pi(s_4|s_2) \\ p_\pi(s_1|s_3) & p_\pi(s_2|s_3) & p_\pi(s_3|s_3) & p_\pi(s_4|s_3) \\ p_\pi(s_1|s_4) & p_\pi(s_2|s_4) & p_\pi(s_3|s_4) & p_\pi(s_4|s_4) \end{pmatrix} \begin{pmatrix} v_1 \\ v_2 \\ v_3 \\ v_4 \end{pmatrix} $$ $$ v_\pi = r_\pi + \lambda P_\pi v_\pi \tag{3} $$

求解

通过贝尔曼方程我们可以求解到每一个状态的状态值，通过（3）式我们可以很容易得到: $$ v_\pi = (I-\lambda P)^{-1}r_\pi $$ 但是当状态空间足够大，\(P\)矩阵的维度将会非常大，对其求逆会消耗大量的计算资源，因此更常用的求解方式是迭代式算法，该算法会生成一个序列 \(v_0,v_1,v_2,…,v_n\)，\(v_0\)是一个初始化的值，通过这个随机值我们可以根据（2）式以此计算出后面的状态值。

迭代式算法有一个重要的特征，也就是当\(n\)趋近于无穷的时候，\(v_{n+1}\)和\(v_n\)基本上相同，其原因这里不做交代。

Action value

很简单，行为值指的就是每一个状态下采取具体的某一个动作能得到的Return, 其实也就是Q-learning中大Q值，也叫动作值函数：

$$ Q_\pi(s,a) = q_\pi(s,a) = \mathbb{E}[G_t|S_t=t,A_t=a] \tag{4} $$

通过行为值的比较，我们可以确定该状态下应该选择具体哪一个行为，一个状态下所有的行为值加起来就等于这个状态的状态值。

根据Return的定义（2）式，我们（4）式展开可以得到：

$$ q_\pi(s,a) = \mathbb{E}[r + \lambda G_{t+1}|S_t=t,A_t=a] \tag{5} $$