在学习TD7算法的时候遇到了Huber Loss，记录一下它与之前我所用的基础的MAE和MSE的不同。

MAE，MSE

MAE（mean absolute error），即平均绝对值误差，也可以看作L1损失，是一种回归模型的常用损失函数，它计算的是目标值和预测值之差的绝对值之和，公式如下：

$$ \text{MAE} = \frac{1}{n}\sum_{i=1}^{n} \left| y_i - y_i^p \right| $$

也就是只衡量了预测值误差的模长而不考虑方向，取值范围也是从0到正无穷。如果考虑模长的话，就变成了MBE，与MAE相比其只少了一个绝对值，但需谨慎使用，因为正负误差可以相互抵消。

$$ \text{MBE} = \frac{1}{n}\sum_{i=1}^{n} (y_i - y_i^p) $$

什么是MSE？Mean squared error，也就是均方误差，类似于L2损失，它求的是预测值与真实值之间距离的平方和，计算公式如下：

$$ \text{MSE} = \frac{1}{n}\sum_{i=1}^{n} (y_i - y_i^p)^2 $$

对比MSE和MAE，可以很轻易地想到，当e>1时 (令e=真实值-预测值)，MSE由于进行了平方操作，它的值会更大，因此MSE对异常点会更加敏感，如果异常点代表很重要的异常情况，并且需要被检测出来，则应选择MSE损失函数。相反，如果异常点是我们不需要的，那么MAE会是个更好的选择。

MAE有一个严重的问题（特别是对于神经网络），就是更新的梯度始终相同，始终为1或者-1，因此必须要结合着变化的学习率来使用才能获得更好的结果。

Huber Loss

Huber loss在MAE和MSE中做平衡，其公式和图像如下所示:

$$ L_\delta(y, f(x)) = \begin{cases} \frac{1}{2}(y - f(x))^2 & \text{for } |y - f(x)| \leq \delta, \\ \delta |y - f(x)| - \frac{1}{2} \delta^2 & \text{otherwise.} \end{cases} $$

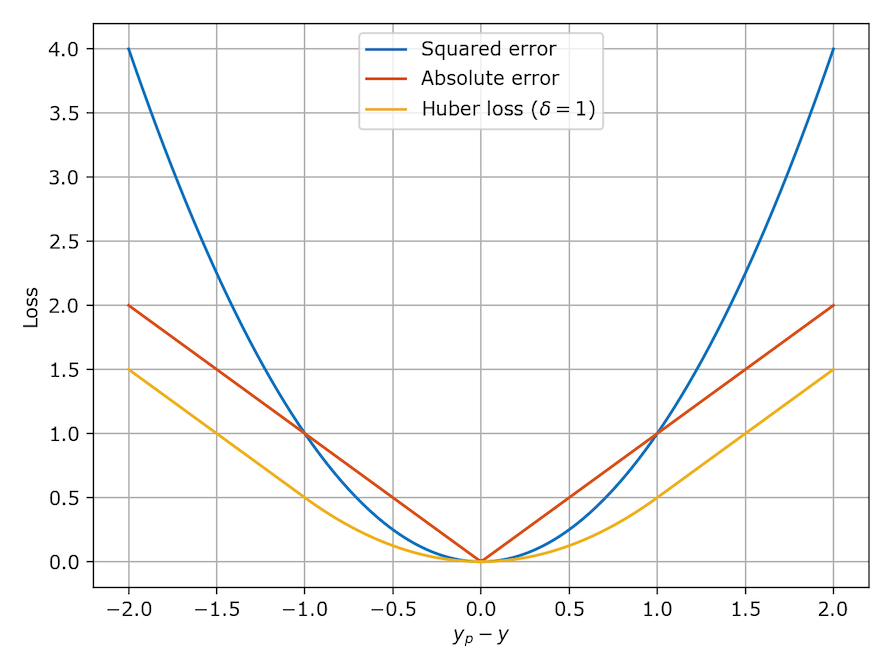
可以看出，当\(|e| \leq \delta\)时，(令e=真实值-预测值)，它采用平方误差，当\(|e| > \delta\)时，转换为线性误差。当\(\delta ～ 0\)的时候，Huber会趋向于MAE，当\(\delta ～ ∞\)的时候，Huber又会趋向于MSE。

Huber损失函数同时具备MSE和MAE这两种损失函数的优点，因为它围绕着最小值会减小梯度，而且相比MSE，它对异常值更具鲁棒性。不过，也存在一个问题，我们可能需要寻找最优的超参数\(\delta\)，比如交叉验证，网格搜索等手段。

通过计算Huber的导数，可以看出来，当\(|e| > \delta\)时，他的导数都会被clip在\(\delta\)，所以当有一些异常值会严重影响模型效率的话，可以以它为根据去设置\(\delta\)值。

# huber 损失
def huber(true, pred, delta):
    loss = np.where(np.abs(true-pred) < delta , 0.5*((true-pred)**2), delta*np.abs(true - pred) - 0.5*(delta**2))
    return np.sum(loss)